개발자L
주 제 : 차원 축소(Dimension Reduction)
작성일 : 2022.02.06
1. 차원 축소(Dimension Reduction)
차원축소란 매우 많은 피처로 구성된 다차원 데이터의 차원을 축소하여 새로운 차원의 데이터를 생성하는 것으로 의미합니다. 일반적으로 수많은 피처로 구성된 데이터셋은 상대적으로 적은 차원에 학습된 모델보다 예측 신뢰도가 떨어지게됩니다. 또한, 피처가 필요이상으로 많은 경우, 피처간의 상관관계가 높아져 모델의 예측 성능이 저하됩니다.
※ 선형회귀에서는 입력변수간의 상관관계를 확인하기위해 다중 공선성(VIF)를 확인하며, 통상 10을 기준점으로 판단함
차원축소는 피처 선택(Feature Selection)과 피처 추출(Feature Extraction)으로 나눌 수 있습니다.
- 피처 선택 : 데이터의 특징을 잘 나태나는 주요 피처만 선택
- 피처 추출 : 기존의 피처(특성)를 저차원의 중요피처로 압축하여 추출
※ 새롭게 추출된 주요 피처는 기존의 피처가 압축된 것으로 기존 피처와는 다른값임
다시말해, 차원축소는 단순히 데이터의 압축을 의미하는 것이 아니라, 축소를 통해 좀 더 데이터를 잘 설명할 수 있는 잠재적인 요소를 추출하는데 있습니다. 이에 PCA, SVD, NMF 알고리즘이 이에 대표적인 예입니다.
2. 주성분 분석 (Principal Component Anaylsis, PCA)
2.1. "주"성분 분석
(가우시안 분포를 따르다는 가정)
주성분분석에 정리가 잘 되어있는 butter shower 블로거님 내용입니다.(하단의 링크 참조)
아래와 같은 저차원의 데이터를 초평면에 투영하게 되면 차원이 감소하게됩니다. 그럼 어떤 초평면을 선택해야하는걸까요?
butter_shower
butter-shower.tistory.com

간단한 2D 데이터셋이 있을 때, 세개의 축을 우리의 초평면 후보로 둡니다. 여기에서 볼 수 있는 것은 실선을 선택하는 방법이 분산을 최대로 보존하는 것이고, c2의 점선을 선택하는 것이 분산을 적게 만들어버리는 방법입니다.
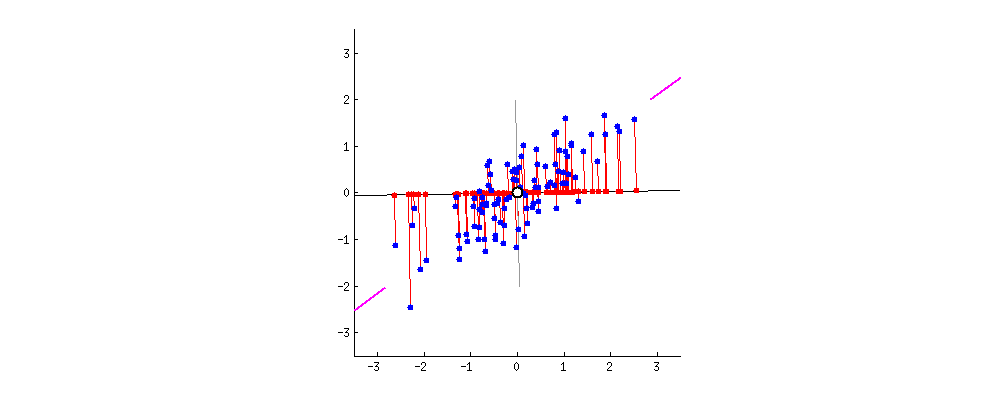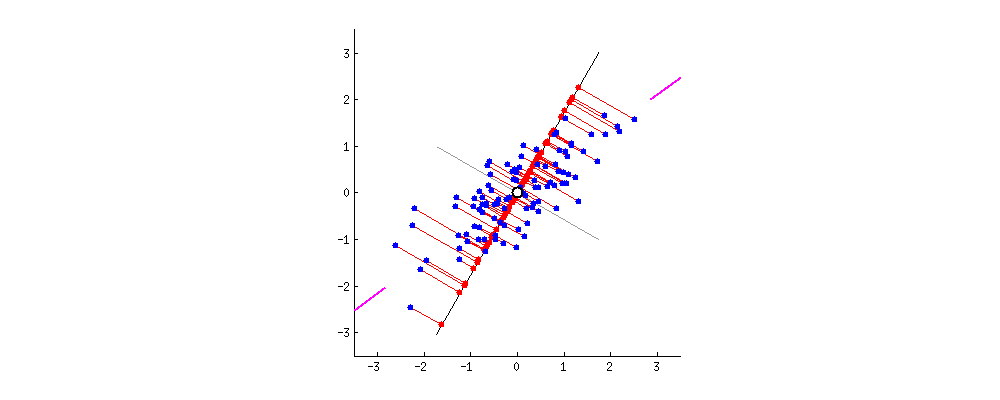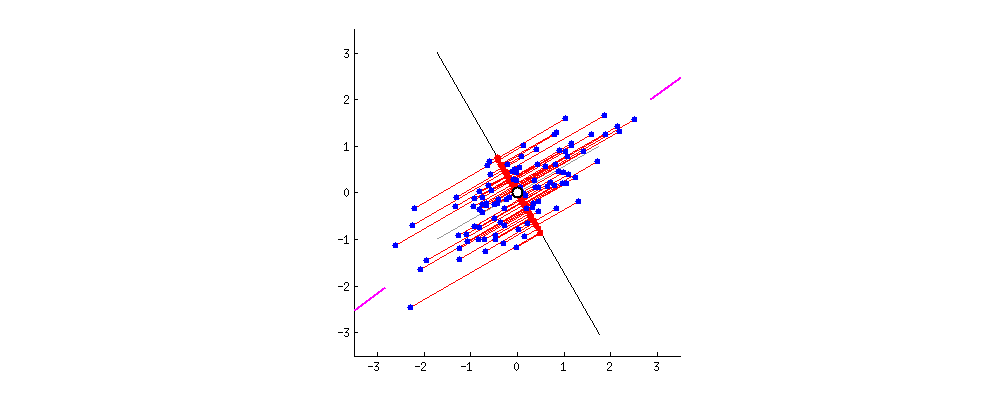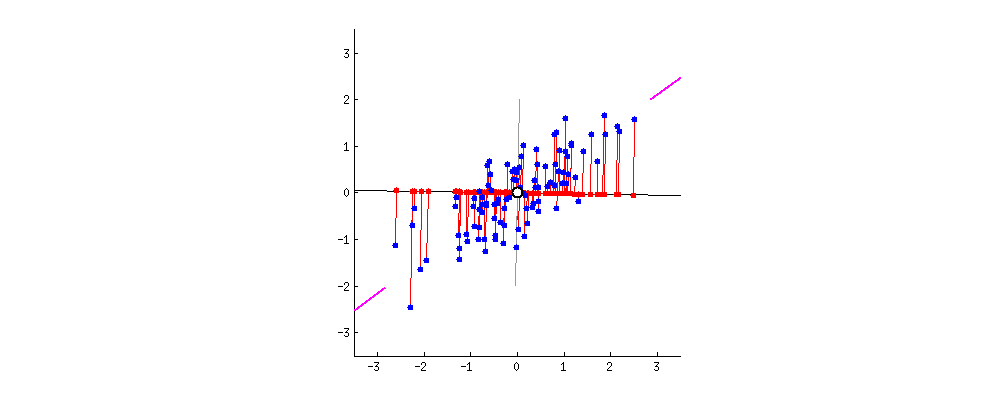
다른 방향으로 투영하는 것 보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있습니다. 분산이 커야 데이터들사이의 차이점이 명확해질테고, 그것이 우리의 모델을 더욱 좋은 방향으로 만들 수 있을 것이기 때문입니다.
2.2. 주성분분석 활용사례
- 영상인식
- 통계데이터분석
- 데이터압축
- 노이즈 제거
3. 선형 판별 분석법(Linear Discriminant Analysis, LDA)
3.1. 주성분분석과 유사한 선형 판별 분석법
LDA는 PCA와 유사하게 입력 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법이지만, 중요한 차이는 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원축소합니다. 이에반해, PCA는 입력 데이터의 변동성의 가장 큰축을 찾습니다. (LDA는 입력데이터의 결정값 클래스를 최대한으로 분리할 수 있는 축을 찾습니다.)
→ 클래스 간 분산은 최대한 크게 가져가나, 클래스 내부의 분산은 최대한 작게 가져가는 방식
※ 선형판별분석법(Linear Discriminat Analysis, LDA)과 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)는 혼동주의
잠재 디리클레 할당은 문서의 주제를 파악하는 자연어 분석과 관련된 알고리즘임 https://lettier.com/projects/lda-topic-modeling/
4. 특이값 분해 (Singular Value Decomposition, SVD)
4.1. 특이값 분해
특잇값 분해(Singular Value Decomposition, SVD)이라는 표준 행렬 분해 기술을 이용해 훈련 세트 행렬 X를 3개의 행렬의 점곱인 U⋅∑⋅VTU⋅∑⋅VT로 분해할 수 있습니다. 여기서 우리가 찾고자하는 모든 주성분은 V에 담겨있습니다.
아래 파이썬 코드는 넘파잉의 svd() 함수를 사용하여 훈련 세트의 모든 주성분을 구한 후 처음 두개의 PC를 추출하는 코드입니다.
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]4.2. 특이값 분해 활용사례
- 이미지 압축을 통한 패턴 인식 및 신호처리
- 텍스트의 토픽 모델링 기법인 LSA(Latent Semantic Anaylsis) 기반 알고리즘
(아래 링크는 LSA(Latent Semantic Anaylsis) 알고리즘과 LDA(Latent Dirichlet Allocation, LDA) 설명)
https://bab2min.tistory.com/585
5. NMF(Non-Negative Matrix Factorizaion)
5.1. 음수를 포함하지않는 행렬 X
음수를 포함하지않은 행렬 X를 음수를 포함하지않는 행렬 W와 H의 곱으로 분해하는 알고리즘이다.
X = W H

5.2. NMF 활용사례
- SVD와 유사하게 이미지 압축을 통한 패턴인식, 텍스터의 토픽 모델링 기법, 문서의 유사도 및 클러스터링
- 영화추천 등의 추천서비스(잠재요소기반의 추천방식)
읽을거리
1. 주성분분석 https://butter-shower.tistory.com/210
2. 선형대수학 https://darkpgmr.tistory.com/110
[선형대수학 #2] 역행렬과 행렬식(determinant)
선형대수학중 역행렬과 행렬식(determinant)에 대한 내용을 주로 활용적인 측면에 초점을 맞추어 적어봅니다. 1. 역행렬(Inverse Matrix)과 선형연립방정식 i) 역행렬의 정의 행렬 A의 역행렬은 A와 곱해
darkpgmr.tistory.com
3. 잠재 디리클레 할당(LDA) https://soojle.gitbook.io/project/requirements/undefined-1/undefined-3/lda
4. 잠재 디리클레 할당 웹사이트에서 적용 https://lettier.com/projects/lda-topic-modeling/
5. NMF 설명(공돌이의 수학정리노트) https://angeloyeo.github.io/2020/10/15/NMF.html
'Python > 2️⃣ 데이터 처리' 카테고리의 다른 글
| [머신러닝] 타이타닉 생존자 예측하기 (0) | 2023.02.06 |
|---|---|
| [머신러닝] 사이킷런으로 시작하는 머신러닝 (0) | 2023.02.06 |
| [알고리즘] 각도기 (0) | 2023.01.12 |
| [Kaggle]Binary classification : Tabular data (0) | 2022.08.15 |
| 머신러닝과 딥러닝의 전반적인 이해 (0) | 2022.01.08 |
