주제: TLE 데이터를 활용한 위성의 위치 예측
작성: 2024-07-14
안녕하세요, 개발자 우성우입니다.
실시간 위성궤도를 알기 위해, 5개의 포스팅을 거쳐 여기까지 왔습니다.
드디어 이번 포스팅에서는 SGP4 활용하여 위성의 위치를 시각화를 구현해 보도록 하겠습니다.
1. SGP4 기본 예제코드
[위성궤도] SGP4 기본 예제코드 이해하기
주제: sg4 라이브러리 활용작성: 2024-07-14SGP4 인공위성의 궤도예측 알고리즘 SGP4(Simplified General Perturbations model 4)는 인공위성의 궤도를 예측하는 알고리즘입니다. 먼저, TLE(Two-Line Element) 데이터를
wscode.tistory.com
2. SGP4 기본 예제코드 업그레이드
오늘 기본예제코드를 변경하여 여러가지를 추가해 보며, 시각화까지 진행해 보고자 합니다
진행 1
import requests
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
from sgp4.api import Satrec, jday
from datetime import datetime, timedelta
import matplotlib.animation as animation
# 위성 TLE 데이터
line1 = "1 33591U 09005A 24189.83565887 .00000265 00000-0 16646-3 0 9998"
line2 = "2 33591 99.0461 245.8524 0013075 231.1406 128.8600 14.13042193794547"
def get_satellite_position(norad_id, dt):
# line1, line2 = fetch_tle(norad_id)
satellite = Satrec.twoline2rv(line1, line2)
jd, fr = jday(dt.year, dt.month, dt.day, dt.hour, dt.minute, dt.second)
e, r, v = satellite.sgp4(jd, fr)
if e != 0:
raise RuntimeError(f"Error in SGP4 propagation: {e}")
return r
def eci_to_geodetic(r):
x, y, z = r
r_e = 6378.137
e2 = 0.08181919**2
lon = np.arctan2(y, x)
lat = np.arctan2(z, np.sqrt(x**2 + y**2))
alt = np.sqrt(x**2 + y**2 + z**2) - r_e
return np.degrees(lat), np.degrees(lon), alt
def calculate_azimuthal_center(lat, lon, alt, azimuth, distance):
"""
위성의 위치와 Azimuth 각도를 이용하여 촬영 중심점을 계산합니다.
"""
# 대략적인 지구 반지름 (km)
R = 6378.137
# 현재 위치에서의 (lat, lon)을 라디안으로 변환
lat_rad = np.radians(lat)
lon_rad = np.radians(lon)
# Azimuth 각도 라디안 변환
azimuth_rad = np.radians(azimuth)
# 위성의 고도까지 포함한 거리 계산
d = (distance / R)
# 중심점 계산
center_lat_rad = np.arcsin(np.sin(lat_rad) * np.cos(d) + np.cos(lat_rad) * np.sin(d) * np.cos(azimuth_rad))
center_lon_rad = lon_rad + np.arctan2(np.sin(azimuth_rad) * np.sin(d) * np.cos(lat_rad), np.cos(d) - np.sin(lat_rad) * np.sin(center_lat_rad))
center_lat = np.degrees(center_lat_rad)
center_lon = np.degrees(center_lon_rad)
return center_lat, center_lon
def calculate_swath_bounds(center_lat, center_lon, swath_width):
"""
촬영 중심점에서 좌우로 Swath 폭 범위를 계산합니다.
"""
delta = swath_width / 2 / 6378.137 # Swath 폭을 라디안으로 변환
min_lat = center_lat - np.degrees(delta)
max_lat = center_lat + np.degrees(delta)
min_lon = center_lon - np.degrees(delta)
max_lon = center_lon + np.degrees(delta)
return (min_lat, max_lat), (min_lon, max_lon)
def animate(i):
dt = start_time + timedelta(minutes=i*interval_minutes)
r = get_satellite_position(norad_id, dt)
lat, lon, alt = eci_to_geodetic(r)
# Azimuth 각도와 거리로 촬영 중심점 계산
azimuth = 45 # 예시로 45도 Azimuth 각도 사용
distance = 500 # 예시로 500km 거리 사용
center_lat, center_lon = calculate_azimuthal_center(lat, lon, alt, azimuth, distance)
# Swath 범위 계산
swath_width = 1000 # 예시로 1000km Swath 폭 사용
(min_lat, max_lat), (min_lon, max_lon) = calculate_swath_bounds(center_lat, center_lon, swath_width)
x, y = m(center_lon, center_lat)
scat.set_offsets([x, y])
time_text.set_text(dt.strftime('%Y-%m-%d %H:%M:%S'))
# Swath 범위 그리기
m.plot([min_lon, max_lon], [min_lat, min_lat], color='blue')
m.plot([min_lon, max_lon], [max_lat, max_lat], color='blue')
m.plot([min_lon, min_lon], [min_lat, max_lat], color='blue')
m.plot([max_lon, max_lon], [min_lat, max_lat], color='blue')
return scat, time_text
norad_id = '33591'
start_time = datetime(2020, 2, 29, 12, 0, 0)
total_minutes_to_animate = 24 * 60 # 24 hours in minutes
interval_minutes = 5 # Update every 5 minutes
# Basemap 초기화
fig = plt.figure(figsize=(10, 7))
m = Basemap(projection='cyl', llcrnrlat=-90, urcrnrlat=90, llcrnrlon=-180, urcrnrlon=180)
m.drawcoastlines()
m.drawcountries()
# 초기 위치 설정
initial_r = get_satellite_position(norad_id, start_time)
initial_lat, initial_lon, initial_alt = eci_to_geodetic(initial_r)
x, y = m(initial_lon, initial_lat)
scat = m.scatter(x, y, color='red', s=100)
time_text = plt.text(-170, -80, '', fontsize=12, color='red')
# 애니메이션 설정
frames = total_minutes_to_animate // interval_minutes
ani = animation.FuncAnimation(fig, animate, frames=frames, interval=200, blit=True)
plt.title('Satellite Position Over Time with Swath Coverage')
ani.save('./Result/Satellite Position Over Time with Swath Coverage.gif', writer='pillow', fps=5)
plt.show()하지만, 극궤도 위성시스템에 익숙하신 분들이란 결과값을 보신들이라면, 잘못된 것을 알 수 있습니다.
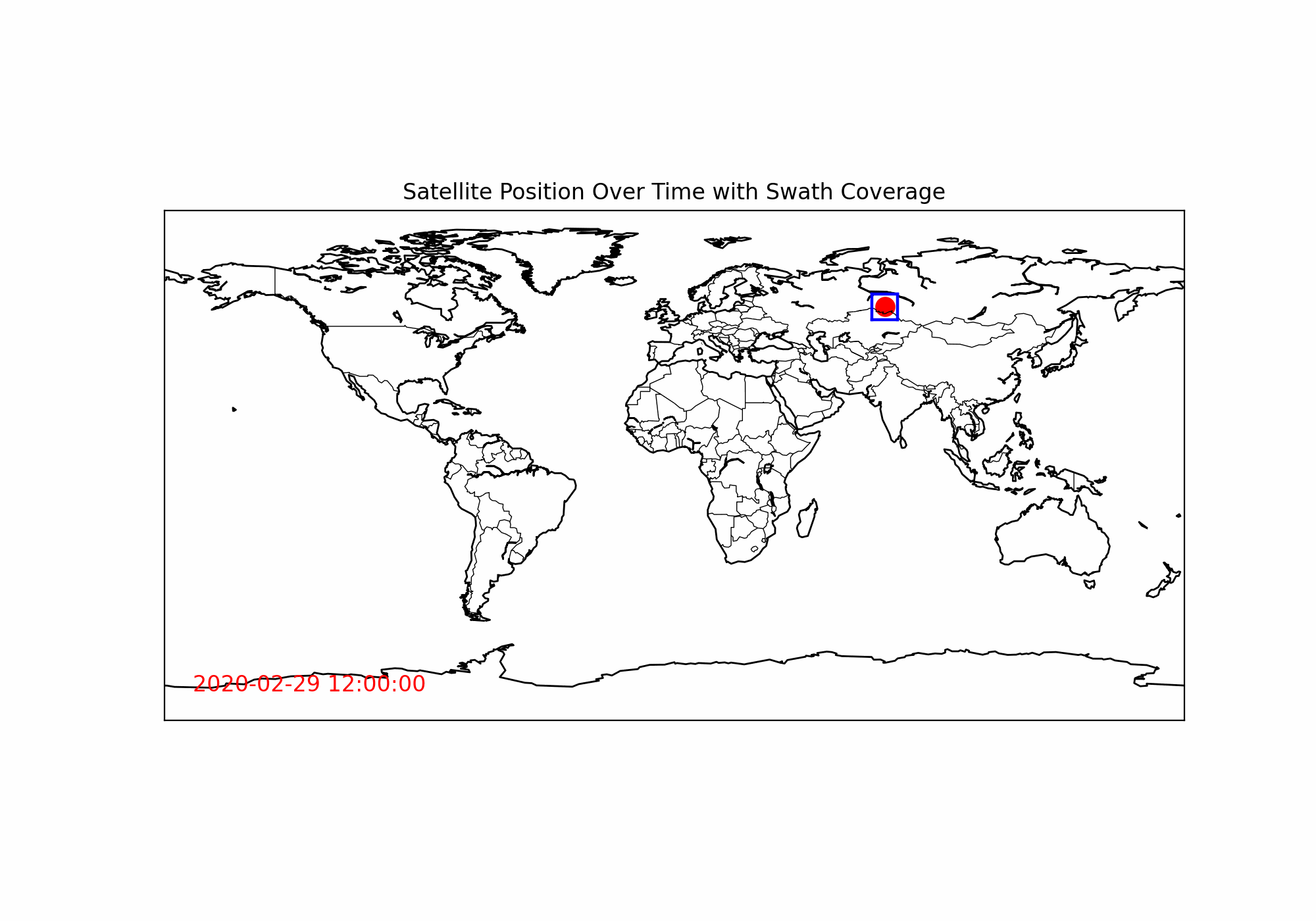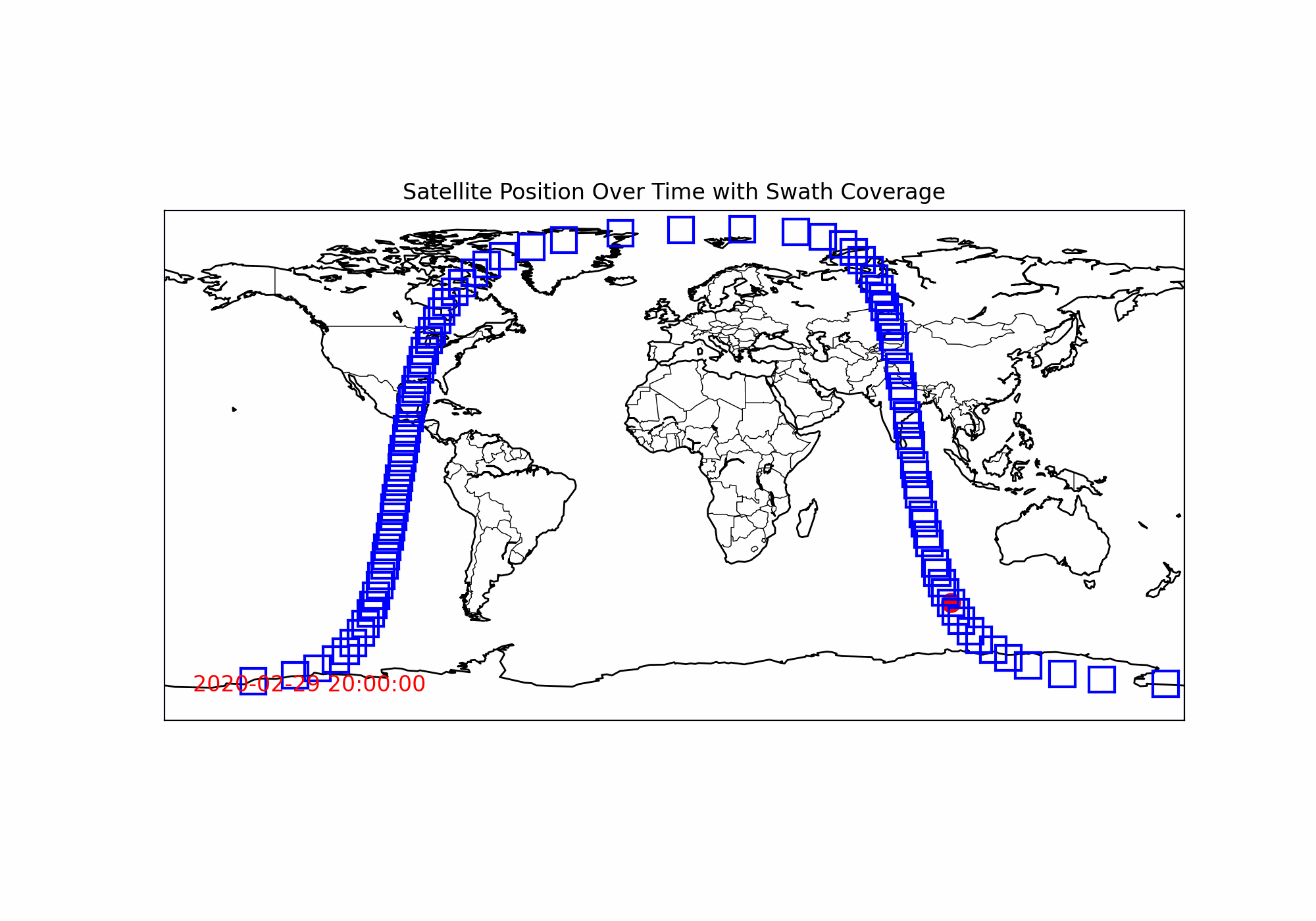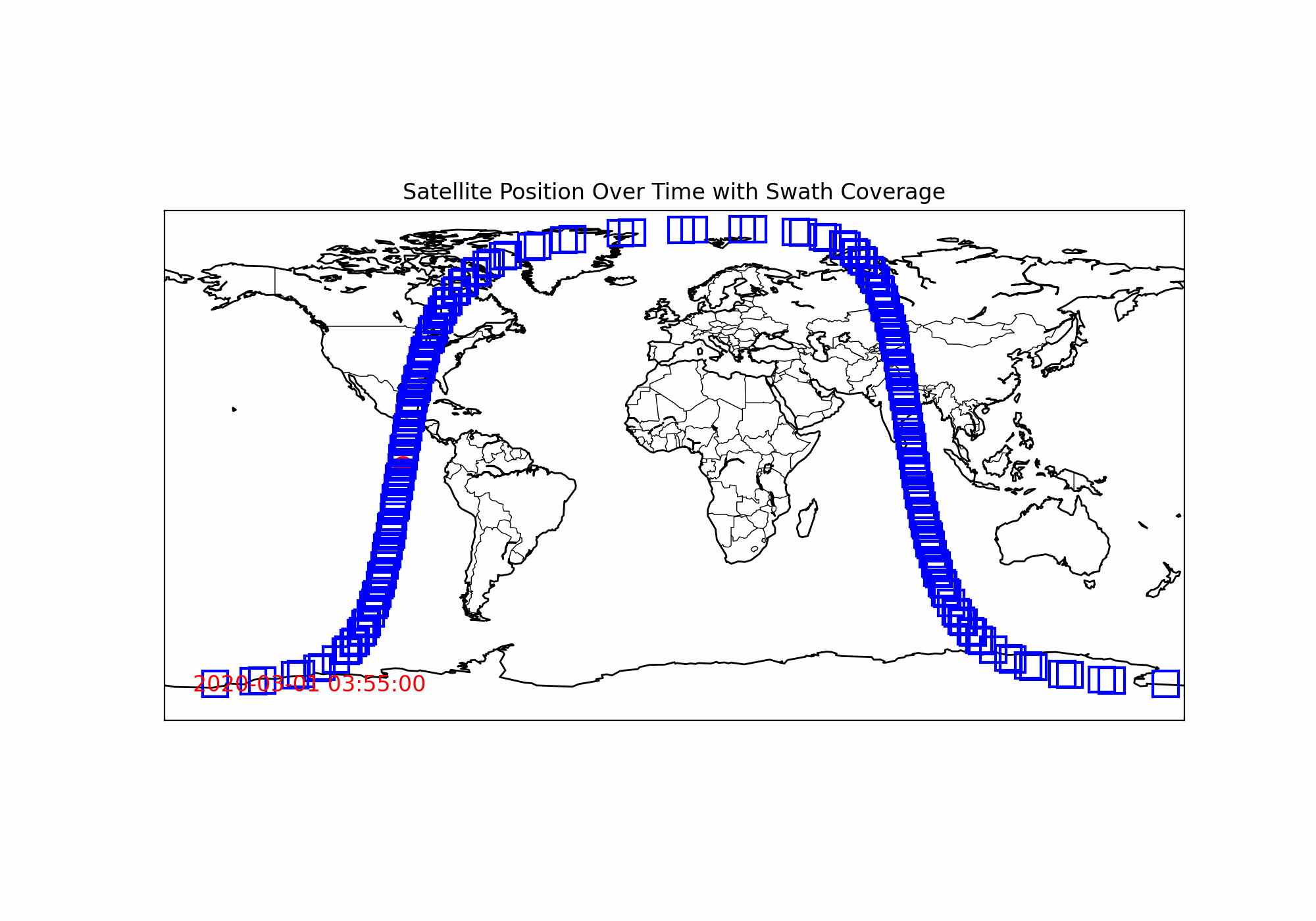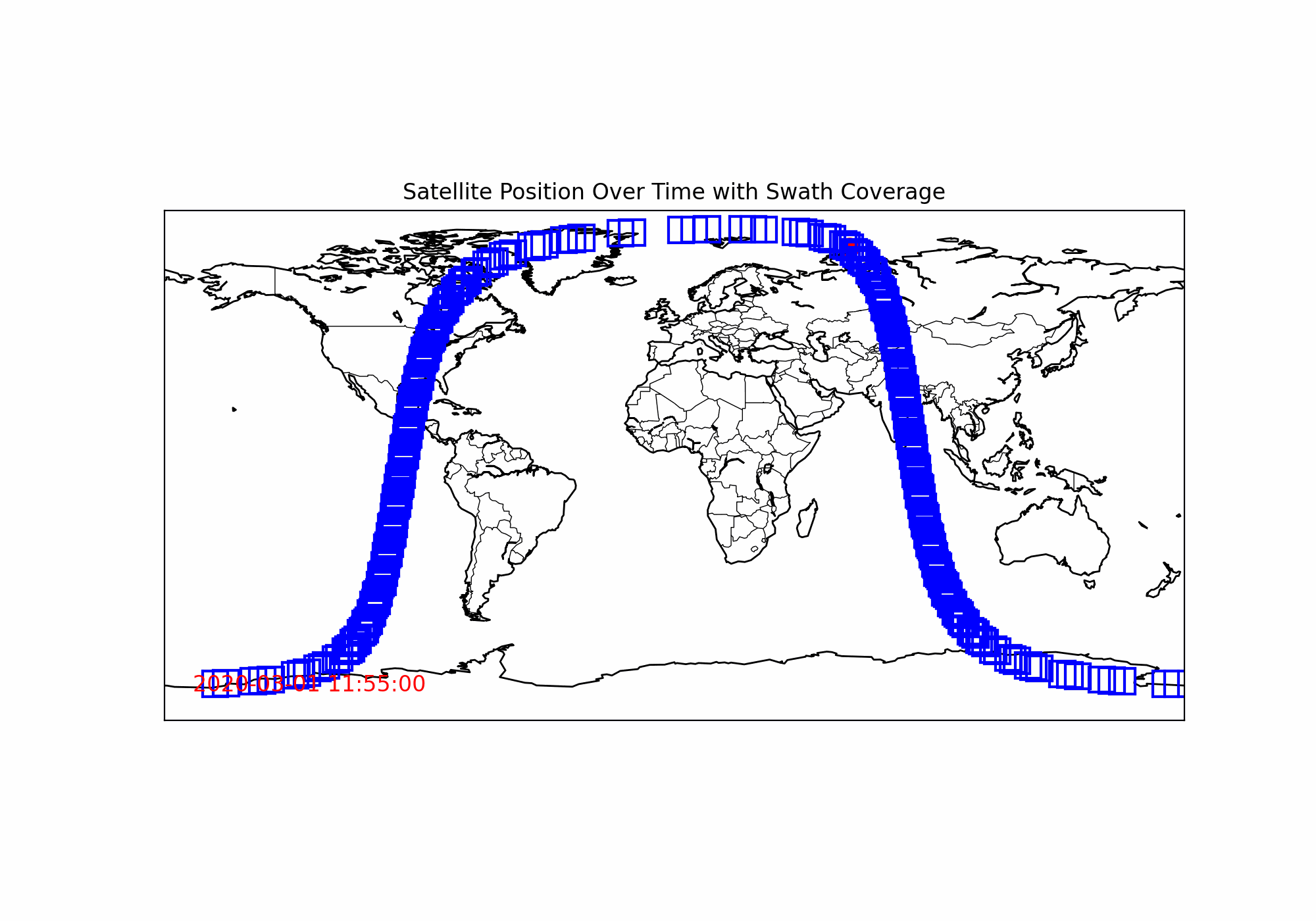
왜 계속 유사한 궤적만 돌고 있지...?
🧑🏻💻 다음 포스팅에서는 🧑🏻💻
많이 왔습니다. 하지만, 아직은 좌표계 변환에 대해 적절하게 적용이 되지 않았기 때문에 값이 생각가 다르게 구현이 되었습니다.
다음 포스팅에서는 좌표계에 대해 이해를 하고 이를 적용시켜 보도록 하겠습니다
'Python > 3️⃣ 프로그래밍' 카테고리의 다른 글
| [위성궤도] SGP4 기본 예제코드 이해하기 (1) | 2024.07.14 |
|---|---|
| [위성궤도] Propagation(전파)와 섭동모델(Perturbations Model) (0) | 2024.07.14 |
| [위성궤도] 넌 또 뭐냐...위성 TLE 데이터 (0) | 2024.07.14 |
| [위성궤도] 위성고유번호 NORAD ID란? (3) | 2024.07.10 |
| [위성궤도] NOAA에서 소유 및 운영 중인 위성들 (1) | 2024.07.09 |
주제: TLE 데이터를 활용한 위성의 위치 예측
작성: 2024-07-14
안녕하세요, 개발자 우성우입니다.
실시간 위성궤도를 알기 위해, 5개의 포스팅을 거쳐 여기까지 왔습니다.
드디어 이번 포스팅에서는 SGP4 활용하여 위성의 위치를 시각화를 구현해 보도록 하겠습니다.

1. SGP4 기본 예제코드
[위성궤도] SGP4 기본 예제코드 이해하기
주제: sg4 라이브러리 활용작성: 2024-07-14SGP4 인공위성의 궤도예측 알고리즘 SGP4(Simplified General Perturbations model 4)는 인공위성의 궤도를 예측하는 알고리즘입니다. 먼저, TLE(Two-Line Element) 데이터를
wscode.tistory.com
2. SGP4 기본 예제코드 업그레이드
오늘 기본예제코드를 변경하여 여러가지를 추가해 보며, 시각화까지 진행해 보고자 합니다
진행 1
import requests
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
from sgp4.api import Satrec, jday
from datetime import datetime, timedelta
import matplotlib.animation as animation
# 위성 TLE 데이터
line1 = "1 33591U 09005A 24189.83565887 .00000265 00000-0 16646-3 0 9998"
line2 = "2 33591 99.0461 245.8524 0013075 231.1406 128.8600 14.13042193794547"
def get_satellite_position(norad_id, dt):
# line1, line2 = fetch_tle(norad_id)
satellite = Satrec.twoline2rv(line1, line2)
jd, fr = jday(dt.year, dt.month, dt.day, dt.hour, dt.minute, dt.second)
e, r, v = satellite.sgp4(jd, fr)
if e != 0:
raise RuntimeError(f"Error in SGP4 propagation: {e}")
return r
def eci_to_geodetic(r):
x, y, z = r
r_e = 6378.137
e2 = 0.08181919**2
lon = np.arctan2(y, x)
lat = np.arctan2(z, np.sqrt(x**2 + y**2))
alt = np.sqrt(x**2 + y**2 + z**2) - r_e
return np.degrees(lat), np.degrees(lon), alt
def calculate_azimuthal_center(lat, lon, alt, azimuth, distance):
"""
위성의 위치와 Azimuth 각도를 이용하여 촬영 중심점을 계산합니다.
"""
# 대략적인 지구 반지름 (km)
R = 6378.137
# 현재 위치에서의 (lat, lon)을 라디안으로 변환
lat_rad = np.radians(lat)
lon_rad = np.radians(lon)
# Azimuth 각도 라디안 변환
azimuth_rad = np.radians(azimuth)
# 위성의 고도까지 포함한 거리 계산
d = (distance / R)
# 중심점 계산
center_lat_rad = np.arcsin(np.sin(lat_rad) * np.cos(d) + np.cos(lat_rad) * np.sin(d) * np.cos(azimuth_rad))
center_lon_rad = lon_rad + np.arctan2(np.sin(azimuth_rad) * np.sin(d) * np.cos(lat_rad), np.cos(d) - np.sin(lat_rad) * np.sin(center_lat_rad))
center_lat = np.degrees(center_lat_rad)
center_lon = np.degrees(center_lon_rad)
return center_lat, center_lon
def calculate_swath_bounds(center_lat, center_lon, swath_width):
"""
촬영 중심점에서 좌우로 Swath 폭 범위를 계산합니다.
"""
delta = swath_width / 2 / 6378.137 # Swath 폭을 라디안으로 변환
min_lat = center_lat - np.degrees(delta)
max_lat = center_lat + np.degrees(delta)
min_lon = center_lon - np.degrees(delta)
max_lon = center_lon + np.degrees(delta)
return (min_lat, max_lat), (min_lon, max_lon)
def animate(i):
dt = start_time + timedelta(minutes=i*interval_minutes)
r = get_satellite_position(norad_id, dt)
lat, lon, alt = eci_to_geodetic(r)
# Azimuth 각도와 거리로 촬영 중심점 계산
azimuth = 45 # 예시로 45도 Azimuth 각도 사용
distance = 500 # 예시로 500km 거리 사용
center_lat, center_lon = calculate_azimuthal_center(lat, lon, alt, azimuth, distance)
# Swath 범위 계산
swath_width = 1000 # 예시로 1000km Swath 폭 사용
(min_lat, max_lat), (min_lon, max_lon) = calculate_swath_bounds(center_lat, center_lon, swath_width)
x, y = m(center_lon, center_lat)
scat.set_offsets([x, y])
time_text.set_text(dt.strftime('%Y-%m-%d %H:%M:%S'))
# Swath 범위 그리기
m.plot([min_lon, max_lon], [min_lat, min_lat], color='blue')
m.plot([min_lon, max_lon], [max_lat, max_lat], color='blue')
m.plot([min_lon, min_lon], [min_lat, max_lat], color='blue')
m.plot([max_lon, max_lon], [min_lat, max_lat], color='blue')
return scat, time_text
norad_id = '33591'
start_time = datetime(2020, 2, 29, 12, 0, 0)
total_minutes_to_animate = 24 * 60 # 24 hours in minutes
interval_minutes = 5 # Update every 5 minutes
# Basemap 초기화
fig = plt.figure(figsize=(10, 7))
m = Basemap(projection='cyl', llcrnrlat=-90, urcrnrlat=90, llcrnrlon=-180, urcrnrlon=180)
m.drawcoastlines()
m.drawcountries()
# 초기 위치 설정
initial_r = get_satellite_position(norad_id, start_time)
initial_lat, initial_lon, initial_alt = eci_to_geodetic(initial_r)
x, y = m(initial_lon, initial_lat)
scat = m.scatter(x, y, color='red', s=100)
time_text = plt.text(-170, -80, '', fontsize=12, color='red')
# 애니메이션 설정
frames = total_minutes_to_animate // interval_minutes
ani = animation.FuncAnimation(fig, animate, frames=frames, interval=200, blit=True)
plt.title('Satellite Position Over Time with Swath Coverage')
ani.save('./Result/Satellite Position Over Time with Swath Coverage.gif', writer='pillow', fps=5)
plt.show()하지만, 극궤도 위성시스템에 익숙하신 분들이란 결과값을 보신들이라면, 잘못된 것을 알 수 있습니다.

왜 계속 유사한 궤적만 돌고 있지...?
🧑🏻💻 다음 포스팅에서는 🧑🏻💻
많이 왔습니다. 하지만, 아직은 좌표계 변환에 대해 적절하게 적용이 되지 않았기 때문에 값이 생각가 다르게 구현이 되었습니다.
다음 포스팅에서는 좌표계에 대해 이해를 하고 이를 적용시켜 보도록 하겠습니다
'Python > 3️⃣ 프로그래밍' 카테고리의 다른 글
| [위성궤도] SGP4 기본 예제코드 이해하기 (1) | 2024.07.14 |
|---|---|
| [위성궤도] Propagation(전파)와 섭동모델(Perturbations Model) (0) | 2024.07.14 |
| [위성궤도] 넌 또 뭐냐...위성 TLE 데이터 (0) | 2024.07.14 |
| [위성궤도] 위성고유번호 NORAD ID란? (3) | 2024.07.10 |
| [위성궤도] NOAA에서 소유 및 운영 중인 위성들 (1) | 2024.07.09 |
